
konstrukce
Konstrukční úlohy
Řešené úlohy
- Příklad č. 1 – Bod v zadané vzdálenosti od přímky a jejího bodu
Je dána přímka p a na ní leží bod P. Sestrojte všechny body, které mají od přímky p vzdálenost 2 cm a od bodu P vzdálenost 4 cm. - Příklad č. 2 – Kružnice procházející zadaným bodem a dotýkající se kružnice
Je dána kružnice k(S; 3 cm) a bod A, kde |SA| = 5 cm. Sestrojte kružnici m(X; 2,5 cm), která se dotýká kružnice k a prochází bodem A. - Příklad č. 3 – Kružnice procházející zadaným bodem A a dotýkající se kružnice v bodě B
Je dána kružnice k(S; 3 cm), bod A, kde |SA| = 5 cm, a bod B, který leží na kružnici k. Sestrojte kružnici m se středem X, která se dotýká kružnice k v bodě B a prochází bodem A. - Příklad č. 4 – Kružnice procházející dvěma zadanými body
Jsou dány body A a B, kde |AB| = 3 cm. Sestrojte kružnici k(S; 2 cm), která oběma body prochází. - Příklad č. 5 – Kružnice dotýkající se dvou různoběžek
Jsou dány různoběžky a, b, které svírají úhel 60°. Sestrojte kružnici k(S; 2 cm), která se obou přímek dotýká. - Příklad č. 6 – Kružnice dotýkající kružnice a přímky
Je dána kružnice k(S; 3 cm) a přímka p ve vzdálenosti 4 cm od bodu S. Sestrojte kružnici m(X; 2 cm), která má s kružnicí k vnější dotyk a dotýká se přímky p.
Co musí obsahovat konstrukční úloha?
- Zadání – stručně si poznačíme zadání, které budeme řešit
- Náčrtek – Načrtneme požadovaný výsledek, zaznačíme údaje, které známe
- Rozbor – od ruky načrtáváme, jak budeme postupovat, vyznačujeme pomocné konstrukce, pojmenováváme jednotlivé konstrukce (přímky, kružnice, …)
- Postup – zapíšeme číslovaný postup, kde musí být patrné, jak jsme postupovali
- Konstrukce – narýsujeme řešení úlohy
- Počet řešení – zapíšeme počet řešení naší úlohy
Jak se píše postup?
V postupu nejprve napíšeme, co je zadáno, včetně rozměrů. Například takto:
Dáno:
Kružnice k(S;3 cm)
Bod X: |SX|=5 cm
Následně zapisujeme postup. Postup je číslovaný a zapsaný tak, že v každém bodě je vždy co rýsujeme, následuje středník a informace o daném objektu. Například, pokud budu rýsovat úsečku AB o délce 5 cm, napíšu následující:
1. AB; |AB| = 5 cm
Posledním bodem postupu je vždy objekt, který jsem chtěl sestrojit – tj. který byl úkolem v zadání. Třeba takto:
5. k(S; 3 cm)
Nejčastější zápisy v postupu
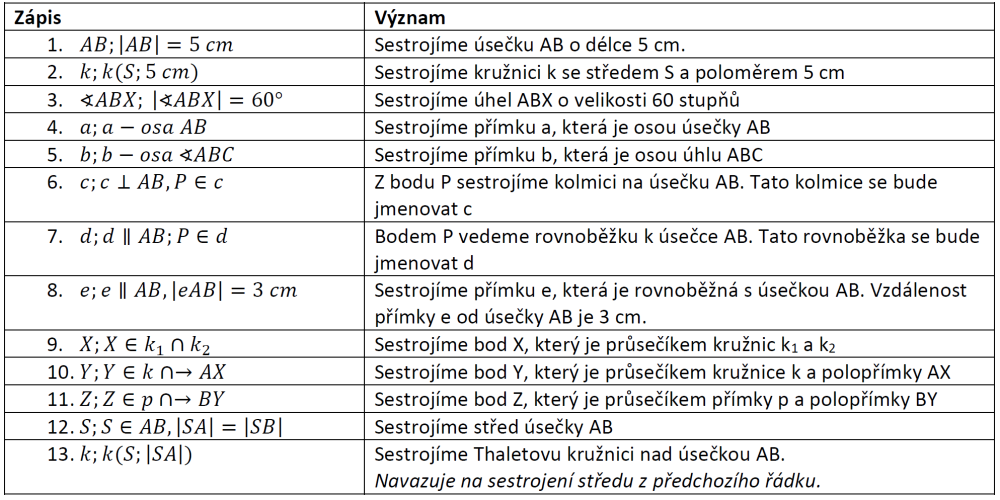
Řešená úloha
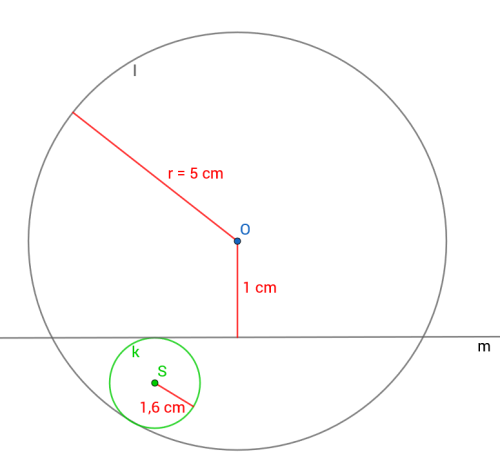
Je dána kružnice l(O;5 cm) a její sečna m. Sestrojte kružnici k se středem S a poloměrem 1,6 cm, která se dotýká přímky m a s kružnicí l má vnitřní dotyk.Vdálenost středu O od přímky m je 1 cm.
Kružnice l(O;5 cm), sečna m, |mO|=1cm.
Sestrojte kružnici k(S;1,6 cm) – dotýká se m a s l má vnitřní dotyk.

Mám dvě podmínky:
1. Kružnice se má dotýkat zadané přímky
2. Kružnice má mít vnitřní dotyk se zadanou kružnicí.
Obě podmínky si převedu na množiny bodů.
Z první podmínky vím, že střed kružnice musí ležet na jedné ze dvou rovnoběžek ve vzdálenosti 1,6 cm – střed kružnice totiž musí ležet 1,6 cm od přímky. – v rozboru červeně
Ze druhé podmínky vím, že střed hledané kružnice musí být 1,6 cm od kružnice (a aby měla vnitřní dotyk, tak uvnitř kružnice). Je to tedy kružnice se středem O a poloměrem 3,4 cm.
A protože musí platit obě podmínky zároveň, najdu průsečík těchto přímek a kružnice (na obrázku označeno S1 a S2. To bude střed hledané kružnice.
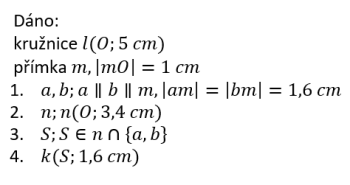
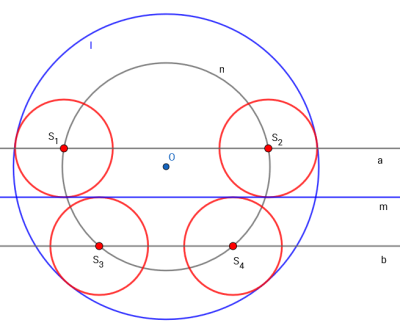
Zadaná úloha má 4 řešení.