konstrukce
Množiny bodů
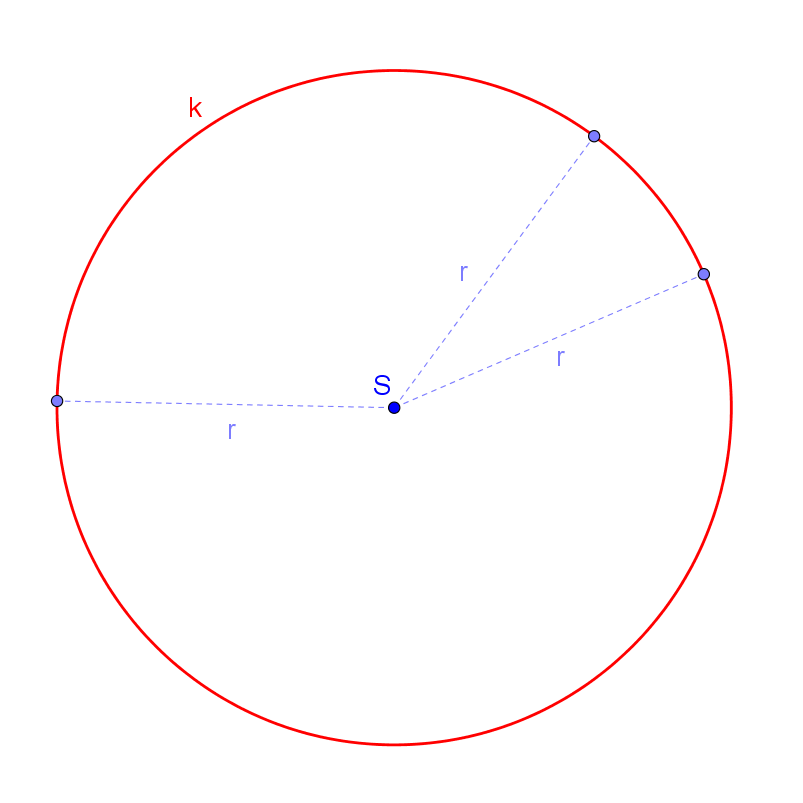
Množina všech bodů, které mají od bodu S vzdálenost rovnu r
Množina všech bodů, které mají od bodu S vzdálenost rovnu r je kružnice k se středem S a poloměrem r.
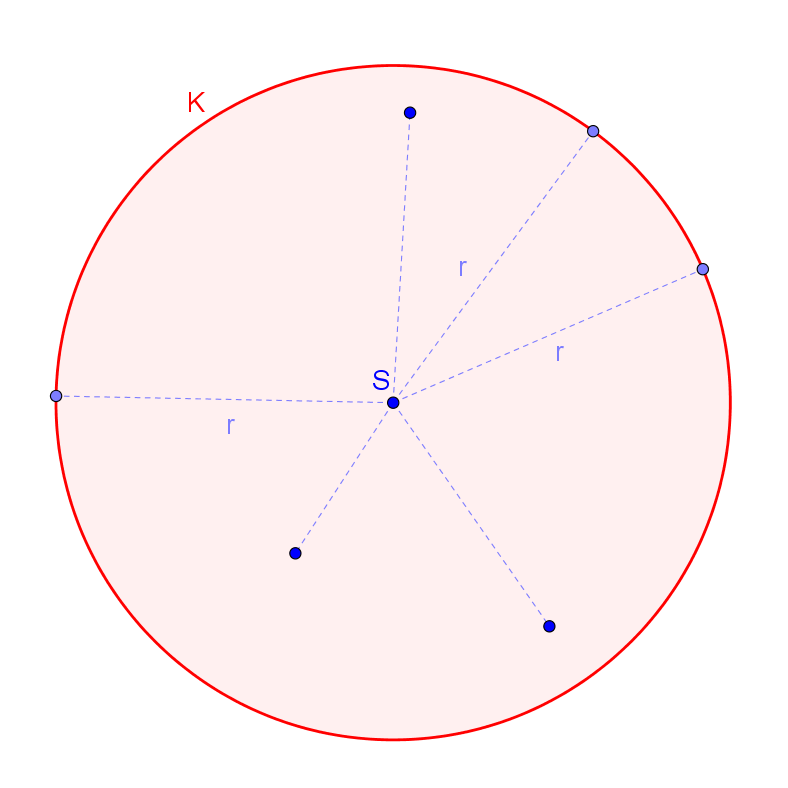
Množina všech bodů, které mají od bodu S vzdálenost menší nebo rovnu r
Množina všech bodů, které mají od bodu S vzdálenost menší nebo rovnu r je kruh K se středem S a poloměrem r.
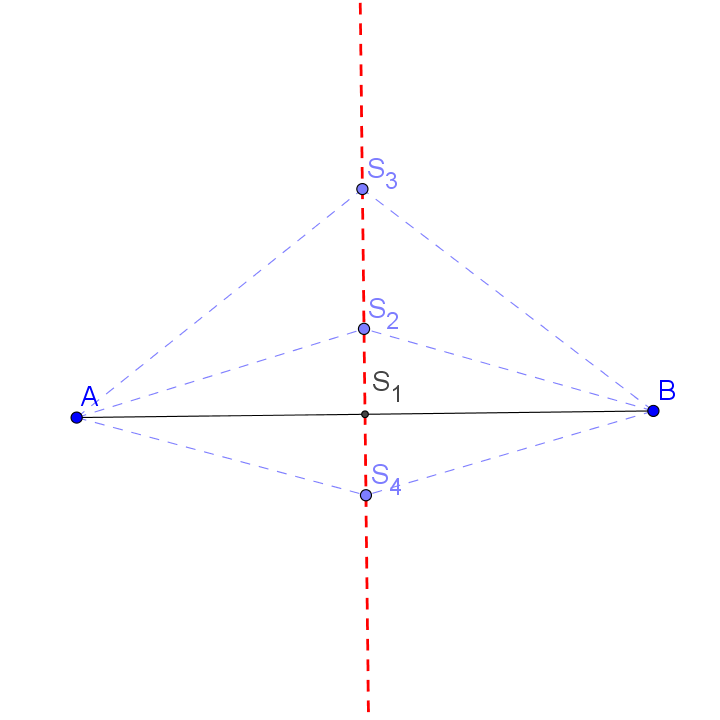
Množina všech bodů, které mají stejnou vzdálenost od dvou daných bodů
Množina všech bodů, které mají stejnou vzdálenost od dvou daných bodů A a B (A ≠ B), je osa úsečky AB.
Množina všech bodů, které mají od dané přímky stejnou vzdálenost
Množina všech bodů, které mají od dané přímky stejnou vzdálenost v je sjednocení dvou rovnoběžek, které mají od dané přímky vzdálenost v.
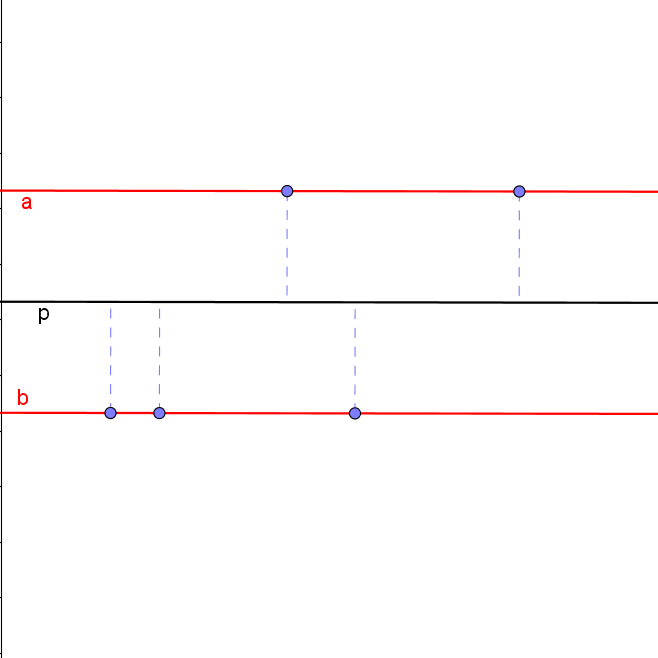
Množina všech bodů, které mají stejnou vzdálenost od dvou daných rovnoběžek
Množina všech bodů, které mají stejnou vzdálenost od dvou daných rovnoběžek, je přímka, která je s nimi rovnoběžná, leží mezi nimi a má od nich stejnou vzdálenost – osa rovinného pásu.
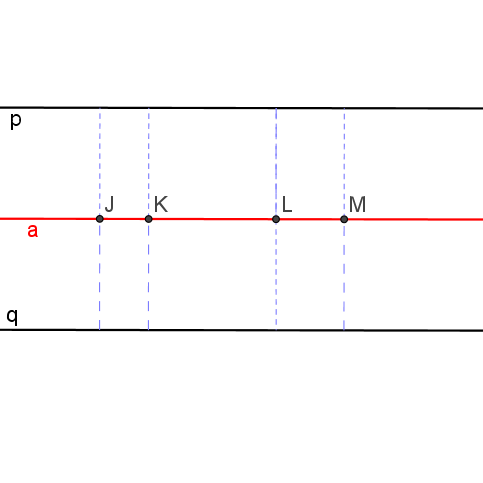
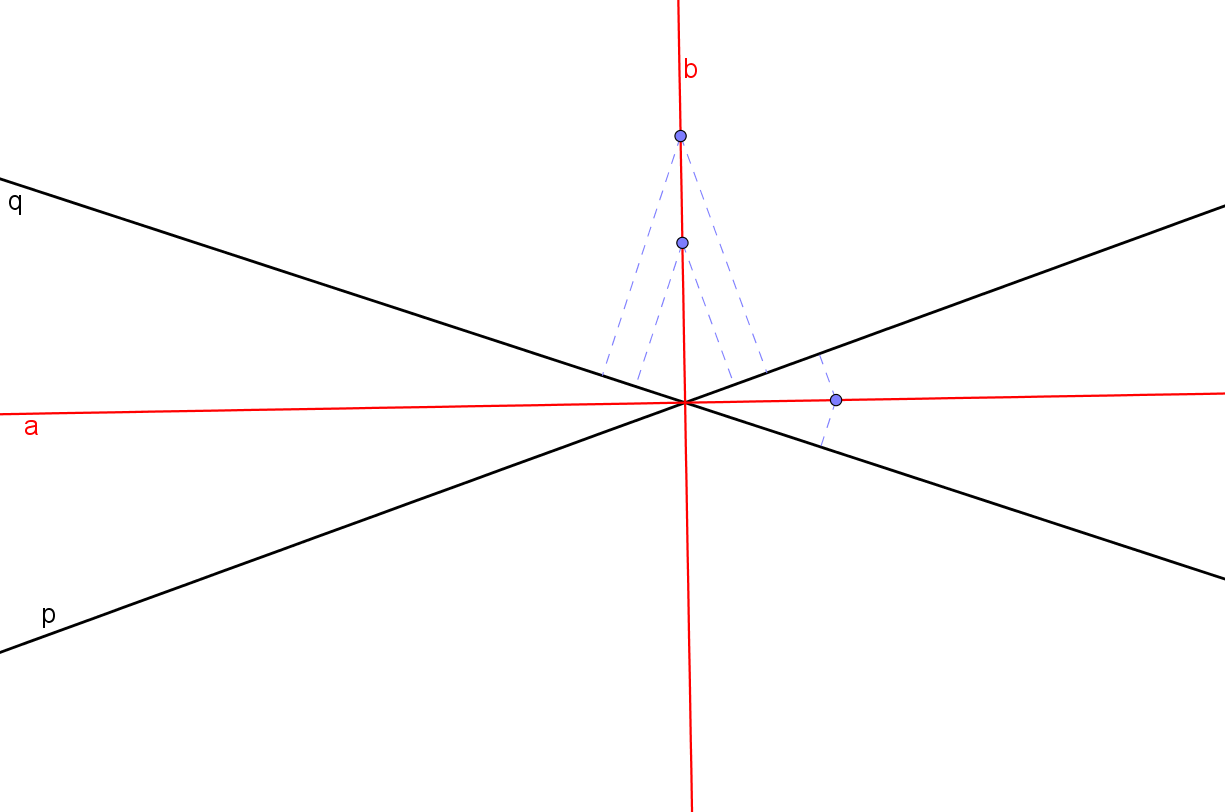
Množina všech bodů, které mají stejnou vzdálenost od dvou daných různoběžek
Množina všech bodů, které mají stejnou vzdálenost od dvou daných různoběžek p a q, je sjednocení dvou navzájem kolmých přímek. Jsou to přímky, na kterých leží osy úhlů vytvořených přímkami p a q.
Množina středů kružnic, které se dotýkají přímky
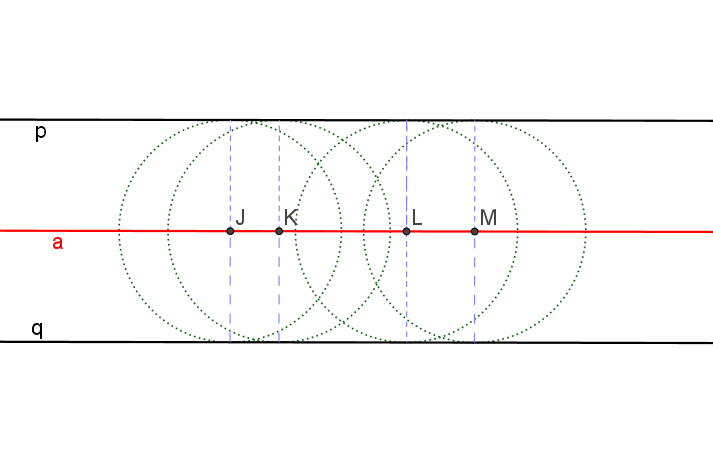
Množina středů kružnic, které se dotýkají přímky je množina všech bodů, které mají od dané přímky vzdálenost r (poloměr kružnice) a je to sjednocení dvou rovnoběžek, které mají od dané přímky vzdálenost r.
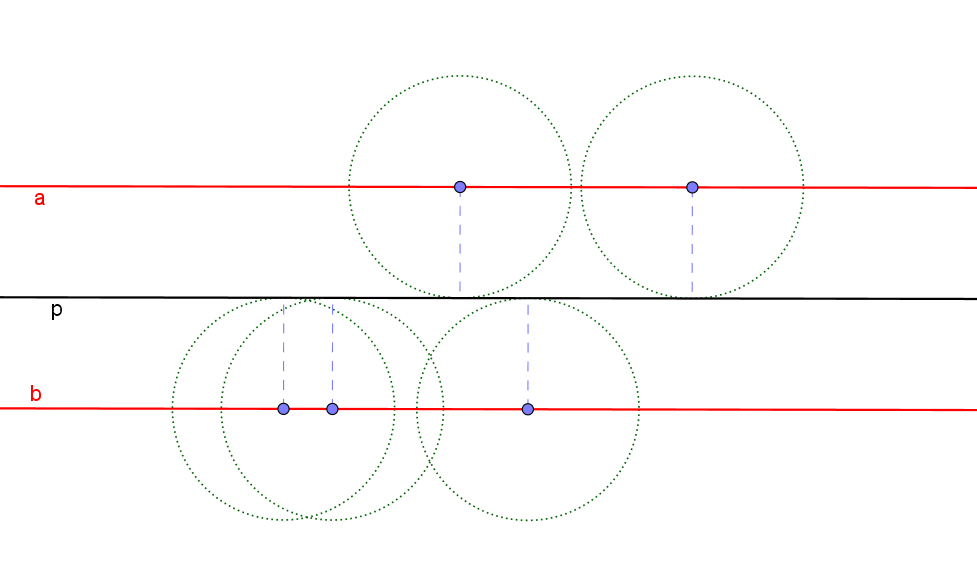
Množina středů kružnic, které se dotýkají dvou rovnoběžek
Množina středů kružnic, které se dotýkají dvou rovnoběžek je množina všech bodů, které mají od dvou daných rovnoběžek stejnou vzdálenost. Je to přímka, která je s nimi rovnoběžná, leží mezi nimi a má od nich stejnou vzdálenost – osa rovinného pásu.
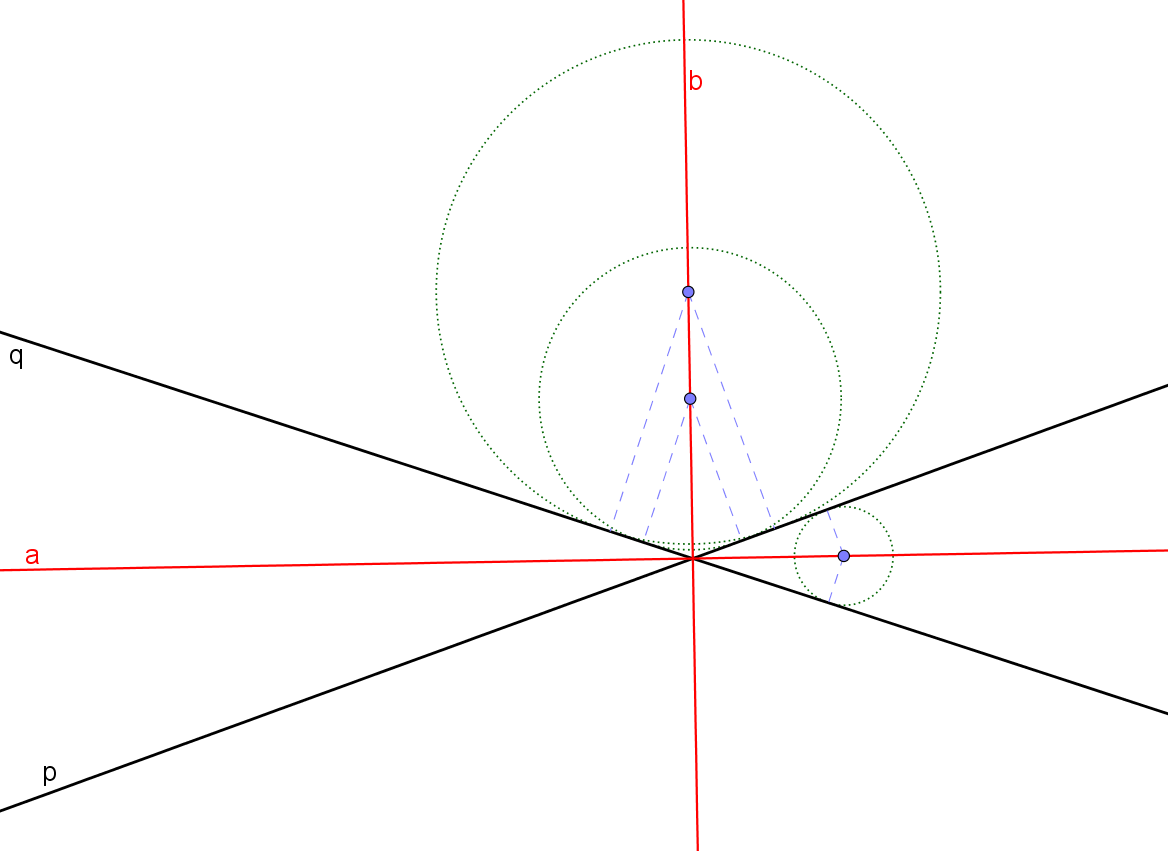
Množina středů kružnic, které se dotýkají dvou různoběžek
Množina středů kružnic, které se dotýkají dvou různoběžek je množina všech bodů, které mají od dvou daných různoběžek p a q stejnou vzdálenost. Je to sjednocení dvou navzájem kolmých přímek. Jsou to přímky, na kterých leží osy úhlů vytvořených přímkami p a q.
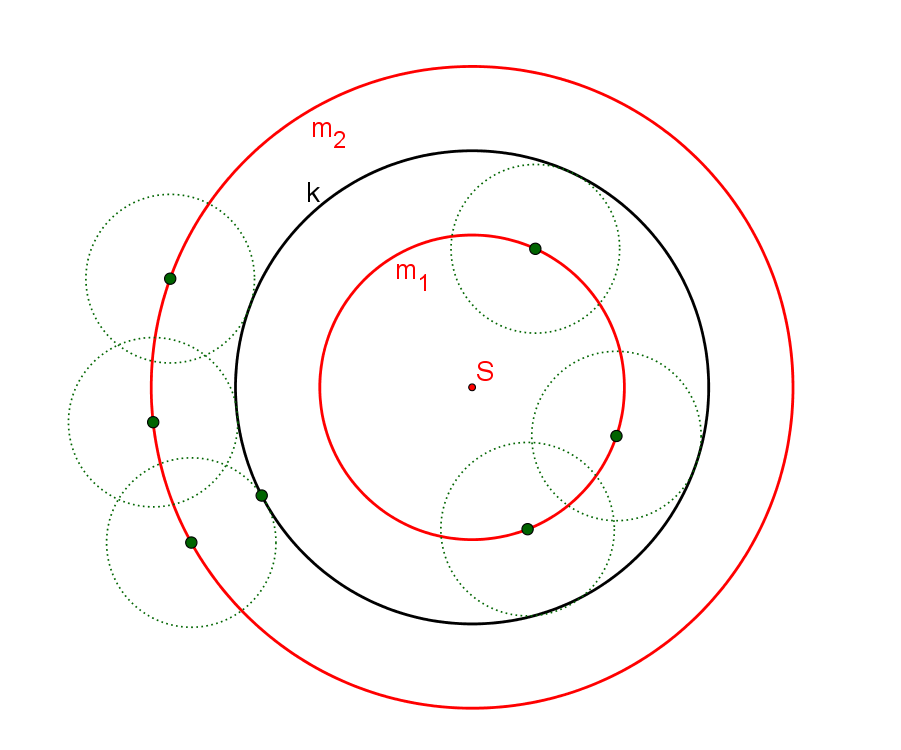
Množina středů všech kružnic, které se dotýkají kružnice
Množina středů všech kružnic o daném poloměru r, které se dotýkají dané kružnice k o středu S a poloměru q, je v případě, že q > r sjednocení dvou soustředných kružnic. Tyto kružnice mají střed S, jejich poloměry jsou q + r a q – r (v případě, že q > r). Pokud q < r, potom tyto kružnice mají střed S, jejich poloměry jsou r + q a r – q.
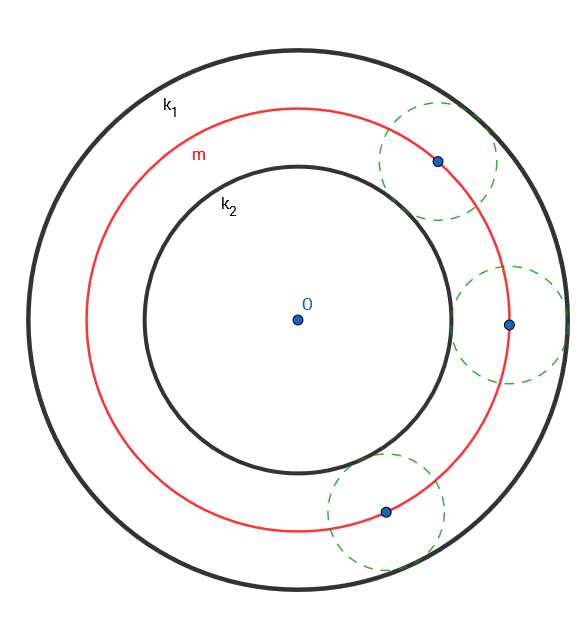
Množina středů všech kružnic, které se dotýkají zadaných soustředných kružnic
Množina středů všech kružnic o daném poloměru r, které se dotýkají kružnic k1 a k2 o středu O a poloměru r1 a r2 (kde r1 > r2), je kružnice se středem O poloměrem (r_1+r_2)/2. Kružnice, které se dotýkají obou zadaných kružnic potom mají poloměr (r_1-r_2)/2.
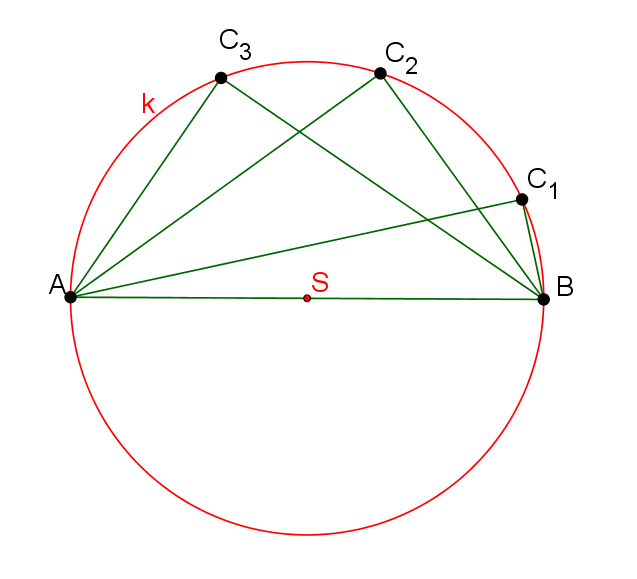
Množina vrcholů C všech pravoúhlých trojúhelníků ABC s danou přeponou AB
Množina vrcholů C všech pravoúhlých trojúhelníků ABC s danou přeponou AB je Thaletova kružnice nad průměrem AB, ze které jsou vyloučeny body A a B.