
a pravděpodobnost
PRAVDĚPODOBNOST
L33: Nezávislé jevy (násobení pravděpodobností)
<< Předchozí lekce | Seznam lekcí | Další lekce >>
Pojmem "Nezávislé jevy" označujeme takové jevy, kdy skutečnost, že nastane jeden jev nemá žádný vliv na to, zda nastane či nenastane jev druhý. Příkladem takových nezávislých jevů může být například opakovaný hod jednou mincí. To, zda padne líc nebo rub při prvním hodu, nijak neovlivní další hody.
Jiná situace by byla v případě náhodného výběru jedné karty z balíčku karet a určení, zda je červená nebo černá s tím, že by se karta do balíčku nevracela. V tomto případě by tahem každé karty v balíčku karet jedna karta ubyla (buď červená nebo černá), což by ovlivnilo pravděpodobnosti v dalších tazích.
Jakým způsobem tedy bude probíhat výpočet u nezávislých jevů?
Pokud máme dva nezávislé jevy $A$ a $B$, určíme jejich pravděpodobnost jako součin pravděpodobností dle vzorce: $${P(A \cap B) = P(A) \cdot P(B)}$$.
Z výše uvedeného vzorce vychází definice nezávislých jevů.
Jevy $A$ a $B$ jsou nezávislé, jestliže platí: $${P(A \cap B) = P(A) \cdot P(B)}$$.
Jevy $A$ , $B$ a $C$ jsou nezávislé, jestliže platí: $${P(A \cap B \cap C) = P(A) \cdot P(B) \cdot P(C)}$$.
Pokud máme 2 nezávislé jevy, budou nezávislé také jevy opačné k nim.
Pokud jsou jevy $A$ a $B$ nezávislé, jsou nezávislé i jevy ${A'}$ a ${B'}$. Stejně to bude platit i pro jevy ${A'}$ a ${B}$ a pro jevy ${A}$ a ${B'}$.
Výrobce uvádí, že jeho pevný disk dokáže fungovat 8000 hodin nepřetržitého provozu s pravděpodobností 95 %.
a) Určete pravděpodobnost nepřetržitého provozu 8000 hodin u diskového pole na serveru, které se skládá ze dvou takových pevných disků.
b) Určete pravděpodobnost nepřetržitého provozu 8000 hodin u diskového pole na serveru, které se skládá ze čtyř takových pevných disků.
a) 2 disky:
$${P(N_1) = 0,95}$$
$${P(N_2) = P(N_1) \cdot P(N_1) = 0,95 \cdot 0,95 = 0,9025}$$
b) 4 disky:
$${P(N_1) = 0,95}$$
$${P(N_4) = P(N_1) \cdot P(N_1) \cdot P(N_1) \cdot P(N_1) = 0,95 \cdot 0,95 \cdot 0,95 \cdot 0,95 = 0,8145}$$
Na daném stroji se vyskytuje závada 1. typu s pravděpodobností 0,25 a závada druhého typu s pravděpodobností 0,2. Obě z těchto závad se vyskytuje s pravděpodobností 0,05. Jedná se o nezávislé jevy?
$${P(A) = 0,25}$$ $${P(B) = 0,2}$$ $${P(A \cap B) = 0,05}$$
Aby se jednalo o nezávislé jevy, musí být splněna podmínka: $${P(A \cap B) = P(A) \dot P(B) = 0,25 \cdot 0,05 = 0,05}$$ Vidíme, že pravděpodobnost průniku jevů je stejná jako zadaná pravděpodobnost, jedná se tedy o nezávislé jevy.
Na daném výrobku se vyskytují 4 druhy vad (označené A, B, C a D). Vada A nastává s pravděpodobností 0,01, vada B s pravděpodobností 0,1, vada C s pravděpodobností 0,2 a vada D s pravděpodobností 0,06. Jaká je pravděpodobnost, že daný výrobek nebude mít žádnou vadu, v případě, že dané vady jsou nezávislé jevy?
Pravděpodobnost, že nastane vada A: ${P(A) = 0,01}$
Pravděpodobnost, že nenastane vada A: ${P(A') = 1 - 0,01 = 0,99}$
Pravděpodobnost, že nastane vada B: ${P(B) = 0,2}$
Pravděpodobnost, že nenastane vada B: ${P(B') = 1 - 0,2 = 0,8}$
Pravděpodobnost, že nastane vada C: ${P(C) = 0,1}$
Pravděpodobnost, že nenastane vada C: ${P(C') = 1 - 0,1 = 0,9}$
Pravděpodobnost, že nastane vada D: ${P(D) = 0,06}$
Pravděpodobnost, že nenastane vada D: ${P(D') = 1 - 0,06 = 0,94}$
Protože se jedná o nezávislé jevy, získáme pravděpodobnost toho, že daný výrobek nebude mít žádnou vadu (zde označené jako jev N), jako součin pravděpodobností, že nenastanou jednotlivé vady.
$${P(N) = P(A') \cdot P(B') \cdot P(C') \cdot P(D') = 0,99 \cdot 0,8 \cdot 0,9 \cdot 0,94 = 0,670032 \doteq 0,67 }$$
Pravděpodobnost, že daný výrobek nebude mít žádnou vadu, bude 0,67.
Elektrický obvod obsahuje 5 spínačů, které náhodně nastavíme do stavu zapnuto nebo vypnuto. Jaká je pravděpodobnost, že obvodem bude procházet elektrický proud?
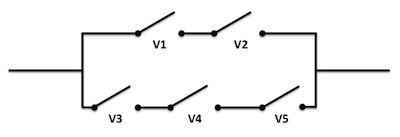
Každou větev elektrického obvodu budeme řešit samostatně. Vypínače v jedné větvi jsou nezávislé, tudíž budeme úkol řešit průnikem pravděpodobností a následně sjednotíme (sečteme) obě větve.
Při výpočtu však musíme zohlednit fakt, že situace, že jsou aktivní obě větve, je v daném součtu započítána dvakrát.
Již jsme používali vzorec pro sjednocení dvou náhodných jevů:
$${P(A \cup B) = P(A) + P(B) - P(A \cap B)}$$
Pravděpodobnost zapnutí jednoho vypínače je ${P(V) = \frac{1}{2}}$
Pravděpodobnost, že bude obvodem procházet elektrocký proud bude: $${P(O) = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} - \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} + \frac{1}{8} - \frac{1}{32} = \frac{11}{32}}$$
Máme balíček 32 karet. Jev A definuje situaci, že náhodně vytažená karta je černá. Jev B definuje situaci, že náhodně vytažená karta je král. Jedná se o nezávislé jevy?
Černých karet je v balíčku polovina, tj. pravděpodobnost vytažení černé karty je: $${P(A) = \frac{1}{2}}$$
Králové jsou v balíčku 4, tj. pravděpodobnost vytažení krále je: $${P(A) = \frac{4}{32} = \frac{1}{8}}$$
Pokud budeme chtít vytáhnout černého krále, tak takové karty máme v balíčku 2: $${P(A \cap B) = \frac{2}{32} = \frac{1}{16}}$$
Aby se jednalo o nezávislé jevy, musí platit: $${P(A \cap B) = P(A) \cdot P(B)}$$ $${\frac{1}{16} = \frac{1}{2} \cdot \frac{1}{8}}$$ $${\frac{1}{16} = \frac{1}{16}}$$
Zadané jevy jsou nezávislé.
V teorii pravděpodobnosti je narozeninovým problémem (či narozeninovým paradoxem) myšlena pravděpodobnost, že pro skupinu náhodně vybraných 23 (či více) lidí, je více než 50% pravděpodobnost, že nějací dva lidé budou mít narozeniny ve stejný den. Pro 57 a více lidí je ona pravděpodobnost více než 99%, postupně rostoucí až ke 100 % pro 366 lidí (za předpokladu že pracujeme s rokem o 365 dnech).
S narozeninovým paradoxem se můžeme setkat i v oblasti informačních technologií, kde byl využit pro prolomení šifrování tzv. narozeninovým útokem. Vychází z předpokladu, že šifrovací funkce může pro 2 různé vstupy vrátit stejný výsledek.
Jaká je pravděpodobnost, že ve třídě, kde je 26 žáků, mají 2 žáci narozeniny ve stejný den?
Pro řešení úkolu si pomůžeme jevem, kdy žádní 2 žáci nemají narozeniny ve stejný den.
První žák se může narodit v libovolný den: $${P_1 = \frac{365}{365}}$$
Druhý žák se může narodit v libovolný den, kromě dne, kdy se narodil první žák: $${P_2 = \frac{364}{365}}$$
Třetí žák se může narodit v libovolný den, kromě dne, kdy se narodil první nebo druhý žák: $${P_3 = \frac{363}{365}}$$
...
26. žák se může narodit v libovolný den, kromě dne, kdy se narodili ostatní: $${P_{26} = \frac{340}{365}}$$
Protože se jedná o nezávislé jevy, můžeme použít součin pravděpodobností: $${P(N) = P_1 \cdot P_2 \cdot ~ \dots ~ \cdot P_{26} = \frac{365 \cdot 364 \cdot ~ \dots ~ \cdot 340}{365^{26}} }$$
Pravděpodobnost, že se alespoň 2 žáci narodí ve stejný den bude opačná k předchozímu jevu: $${P(S) = 1 - P(N) = 1 - \frac{365 \cdot 364 \cdot ~ \dots ~ \cdot 340}{365^{26}} \doteq 0,6 }$$
- Co jsou to "nezávislé jevy"?
- Jaký vztah platí pro dva nezávislé jevy A a B s pravděpodobností P(A) a P(B)?
- Přístroj se skládá ze 3 samostatných modulů A, B a C. Pravděpodobnost výskytu závady na modulu A je 5 %, na modulu B je 8 % a na modulu C 12 %. Jaká je pravděpodobnost, že přístroj bude fungovat v pořádku, pokud se jedná o nezávislé jevy?
- Pojmem "Nezávislé jevy" označujeme takové jevy, kdy skutečnost, že nastane jeden jev nemá žádný vliv na to, zda nastane či nenastane jev druhý. Příkladem takových nezávislých jevů může být například opakovaný hod jednou mincí.
- $${P(A \cap B) = P(A) \cdot P(B)}$$
- Pravděpodobnost bezchybného provozu je $${0,76912}$$