
a pravděpodobnost
KOMBINATORIKA
L09: Pascalův trojúhelník
<< Předchozí lekce | Seznam lekcí | Další lekce >>
V lekci, která se týká vlastností kombinačních čísel, jsme se seznámili s několika důležitými vlastnostmi, které můžeme využít ke konstrukci tzv. Pascalova trojúhelníku, jehož autorem je Blaise Pascal.

Blaise Pascal se narodil v Clermont-Ferand ve Francii ve vzdělané rodině známého matematika Etienna a Antoinette Pascalových. Matka brzy zemřela a otec, který se roku 1631 přestěhoval s dětmi do Paříže, mu poskytl vynikající humanitní vzdělání. I když sám byl dobrým matematikem, před chlapcem tuto vědu zatajil. Musel však kapitulovat, když zjistil, že asi desetiletý Blaise už si sám odvodil několik vět Eukleidovy geometrie. Roku 1638 se jeho otec – správce královských daní - dostal do konfliktu s kardinálem Richelieu kvůli novým daním a odstěhoval se do Rouenu; pro něho Blaise zkonstruoval svůj počítací stroj.
V 17 letech napsal Pojednání o kuželosečkách, které ocenila Pařížská královská akademie a Descartes je pokládal za práci jeho otce. Věnoval se především geometrii, kde objevil tzv. Pascalovu větu o vztazích mezi body na kuželosečkách. Jedná se o zobecnění tzv. Pappovy úlohy, jíž se zabýval také Descartes a jejíž vyřešení pokládal za doklad, že jeho současníci překonali staré Řeky. Pascal také významně přispěl k rozvoji kombinatoriky, když objevil tzv. Pascalův trojúhelník, který má využití také v algebře. Se svým přítelem Pierre De Fermatem definoval základy teorie pravděpodobnosti.
V oblasti fyziky navázal na Torricelliho pokusy se rtuťovou trubicí. Jeho další pokusy se týkaly spojitých nádob a šíření tlaku v kapalinách, kde formuloval tzv. Pascalův princip (tlak v kapalině se šíří všemi směry stejně). Na jeho byla po něm pojmenována jednotka tlaku.
Při konstrukci tohoto trojúhelníku využijeme vzorec ${\binom{n}{k} + \binom{n}{k + 1} = \binom{n + 1}{k + 1}}$. Tento trojúhelník je totiž zkonstruován tak, že na prvním řádků je kombinační číslo ${\binom{0}{0}}$, na druhém ${\binom{1}{0}}$ a ${\binom{1}{1}}$, na třetím ${\binom{2}{0}}$, ${\binom{2}{1}}$ a ${\binom{2}{2}}$, atd. Lze tedy říct, že každé kombinační číslo v Pascalově trojúhelníku je tvořeno součtem dvou čísel, které má nad sebou, což je ještě patrnější, když se v tomto trojúhelníku zobrazí přímo hodnoty těchto kombinačních čísel (na obvodu budou hodnoty 1, ostatní hodnoty budou součty dvou hodnot z předchozího řádku).

Určete hodnoty na 7. řádku Pascalova trojúhelníku.
7. řádek Pascalova trojúhelníku je tvořen kombinačními čísly $${\binom{7}{0}, \binom{7}{1}, \binom{7}{2}, \binom{7}{3}, \binom{7}{4}, \binom{7}{5}, \binom{7}{6}, \binom{7}{7}}$$
Díky platnosti vztahu ${\binom{n}{k} = \binom{n}{n-k}}$ není nutné počítat všechny hodnoty, protože hodnoty v Pascalově trojúhelníku jsou rozmístěny symetricky.
$${\binom{7}{0} = \binom{7}{7} = 1}$$
$${\binom{7}{1} = \binom{7}{6} = 7}$$
$${\binom{7}{2} = \binom{7}{5} = \frac{7!}{5!\cdot(7-5)!} = \frac{7!}{5!\cdot2!} = \frac{7 \cdot 6}{2} = 21}$$
$${\binom{7}{3} = \binom{7}{4} = \frac{7!}{3!\cdot(7-3)!} = \frac{7!}{3!\cdot4!} = \frac{7 \cdot 6 \cdot 5}{3 \cdot 2} = 35}$$
Na 7. řádku Pascalova trojúhelníku budou hodnoty 1, 7, 21, 35, 35, 21, 7 a 1.
Určete hodnoty na 15. řádku Pascalova trojúhelníku.
15. řádek Pascalova trojúhelníku je tvořen kombinačními čísly $${\binom{15}{0}, \binom{15}{1}, \binom{15}{2}, \binom{15}{3}, \dots, \binom{15}{15}}$$
Díky platnosti vztahu ${\binom{n}{k} = \binom{n}{n-k}}$ není nutné počítat všechny hodnoty, protože hodnoty v Pascalově trojúhelníku jsou rozmístěny symetricky.
$${\binom{15}{0} = \binom{15}{15} = 1}$$
$${\binom{15}{1} = \binom{15}{14} = 15}$$
$${\binom{15}{2} = \binom{15}{13} = \frac{15!}{2!\cdot(15-2)!} = \frac{15!}{2!\cdot13!} = 105}$$
$${\binom{15}{3} = \binom{15}{12} = \frac{15!}{3!\cdot(15-3)!} = \frac{15!}{3!\cdot12!} = 455}$$
$${\binom{15}{4} = \binom{15}{11} = \frac{15!}{4!\cdot(15-4)!} = \frac{15!}{4!\cdot11!} = 1365}$$
$${\binom{15}{5} = \binom{15}{10} = \frac{15!}{5!\cdot(15-5)!} = \frac{15!}{5!\cdot10!} = 3003}$$
$${\binom{15}{6} = \binom{15}{9} = \frac{15!}{6!\cdot(15-6)!} = \frac{15!}{6!\cdot9!} = 5005}$$
$${\binom{15}{7} = \binom{15}{8} = \frac{15!}{7!\cdot(15-7)!} = \frac{15!}{7!\cdot8!} = 6435}$$
Na 7. řádku Pascalova trojúhelníku budou hodnoty 1, 15, 105, 455, 1365, 3003, 5005, 6435, 6435, 5005, 3003, 1365, 455, 105, 15 a 1.
Určete hodnoty na 9. řádku Pascalova trojúhelníku, pokud víte, že 8. řádek je tvořen hodnotami 1, 8, 28, 56, 70, 56, 28, 8, 1.
Víme, že krajní hodnoty v Pascalově trojúhelníku jsou hodnoty 1 a každá další hodnota je součtem hodnot, které má v trojúhelníku nad sebou.
1. hodnota ... 1
2. hodnota ... 1 + 8 = 9
3. hodnota ... 8 + 28 = 36
4. hodnota ... 28 + 56 = 84
5. hodnota ... 56 + 70 = 126
6. hodnota ... 70 + 56 = 126
7. hodnota ... 56 + 28 = 84
8. hodnota ... 28 + 8 = 36
9. hodnota ... 8 + 1 = 9
10. hodnota ... 1
Na 9. řádku Pascalova trojúhelníku budou hodnoty 1, 9, 36, 84, 126, 126, 84, 36, 9 a 1.
Zajímavou informací je i součet hodnot kombinačních čísel v jednom řádku Pascalova trojúhelníku.
Pro řádek č. 0 je to 1
Pro řádek č. 1 je to 1 + 1 = 2
Pro řádek č. 2 je to 1 + 2 + 1 = 4
Pro řádek č. 3 je to 1 + 3 + 3 + 1 = 8
Pro řádek č. 4 je to 1 + 4 + 6 + 4 + 1 = 16
Z výše uvedeného postupu je viditelné, že součet hodnot v řádku Pascalova trojúhelníku je n-tá mocnina 2.
Jaký je součet hodnot na 9. řádku Pascalova trojúhelníku?
$${p = 2^9 = 512}$$
Další využití Pascalova trojúhelníku lze nalézt u hledání počtu cest ve čtvercové síti.
Ulice ve městě tvoří pravoúhlou čtvercovou síť (jak je viditelné na níže uvedené pláni). Určete, kolika způsoby se lze dostat z místa A do místa B (Madison Square Park), pokud se smíme pohybovat jen směrem doprava a nahoru?
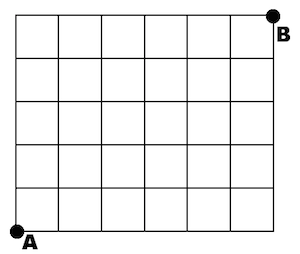
Když se podíváme na níže uvedený obrázek, zjistíme, že z bodu A se do vedlejších uzlů dostaneme jedním způsobem, do uzlu který se nachází mezi nimi dvěma apod.
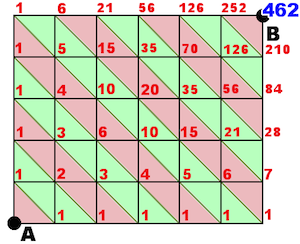
Zajímavostí je, že počty možných cest tvoří řádky Pascalova trojúhelníku (na obrázku barevně odlišeny).
Pokud má daná síť m řádků a n sloupců platí, že počet cest je ${\binom{m + n}{n}}$ nebo ${\binom{m + n}{m}}$, kde m je počet čar mezi uzly ve vodorovném směru a n je počet čar mezi uzly ve svislém směru.
$${\binom{m + n}{n} = \binom{6 + 5}{5} = \binom{11}{5} = \frac{11!}{5! \cdot 6!} = 462}$$
Existuje 462 způsobů, jak se dostat z místa A do místa B tak, že se pohybujeme jen směrem doprava a nahoru (viz následující obrázek).

Kromě hodnot kombinačních čísel můžeme v Pascalově trojúhelníku najít i určitou geometrickou strukturu. Pokud všechna sudá čísla vybarvíme jednou barvou a lichá čísla jinou, získáme útvar zvaný Sierpinského trojúhelník, což je jeden z fraktálních útvarů.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
... ... ...
Fraktál - je to nekonečně členitý útvar (když jej neustále zvětšujeme, nacházíme v něm opakující se strukturu). Objevitelem fraktálů je vědec polského původu Benoit B. Mandelbrot. Tyto útvary nachází uplatnění zejména v počítačové grafice.
Mezi nejznámější fraktály patří např. Kochova vločka, Mandelbrotova množina nebo Sierpinského kobereček.
- Jak jsou tvořeny hodnoty v Pascalově trojúhelníku?
- Jaké hodnoty budou na 12. řádku Pascalova trojúhelníku?
- Jaký bude součet hodnot na 15. řádku Pascalova trojúhelníku?
- n-tý řádek je tvořen kombinačními čísly $${\binom{n}{0}, \binom{n}{1}, \binom{n}{2}, \dots, \binom{n}{n - 1}, \binom{n}{n}}$$ Každá hodnota je tvořena součtem hodnot, které má v trojúhelníku nad sebou.
- 1, 11, 55, 165, 330, 462, 462, 330, 165, 55, 11, 1
- 32 768