
a pravděpodobnost
PRAVDĚPODOBNOST
L34: Příklady na procvičení XII
<< Předchozí lekce | Seznam lekcí | Další lekce >>
Obyčejná žárovka dokáže svítit bez poruchy po dobu 1000 hodin s pravděpodobností 80 %. S jakou pravděpodobností budou svítit bez poruchy:
a) 2 sériově zapojené žárovky?
b) 3 sériově zapojené žárovky?
Pravděpodobnost závady jedné žárovky: $${P(Z) = 0,8}$$
Při zapojení dvou žárovek: $${P(Z_2) = P(Z) \cdot P(Z) = 0,8 \cdot 0,8 = 0,64}$$
Při zapojení tří žárovek: $${P(Z_3) = P(Z) \cdot P(Z) \cdot P(Z) = 0,8 \cdot 0,8 \cdot 0,8 = 0,512}$$
Ve druhém ročníku střední školy propadá ve čtvrtletí průměrně 2 % žáků z českého jazyka, 5 % žáků z anglického jazyka a 1 % žáků z obou předmětů. Rozhodněte, zda propadnutí z českého jazyka a propadnutí z anglického jazyka jsou nezávislé jevy.
Český jazyk: $${P(A) = 0,02}$$
Anglický jazyk: $${P(B) = 0,05}$$
Český a anglický jazyk: $${P(A \cap B) = 0,01}$$
Aby se jednalo o nezávislé jevy, musí platit: $${P(A \cap B) = P(A) \cdot P(B)}$$ $${0,01 = 0,02 \cdot 0,05}$$ $${0,01 \neq 0,001}$$
Zadané jevy jsou závislé.
Na daném výrobku se vyskytují 3 druhy vad (označené A, B, a C). Vada A nastává s pravděpodobností 0,05, vada B s pravděpodobností 0,06 a vada C s pravděpodobností 0,07. Jaká je pravděpodobnost, že daný výrobek nebude mít žádnou vadu, v případě, že dané vady jsou nezávislé jevy?
Pravděpodobnost, že nastane vada A: ${P(A) = 0,05}$
Pravděpodobnost, že nenastane vada A: ${P(A') = 1 - 0,05 = 0,95}$
Pravděpodobnost, že nastane vada B: ${P(B) = 0,06}$
Pravděpodobnost, že nenastane vada B: ${P(B') = 1 - 0,06 = 0,94}$
Pravděpodobnost, že nastane vada C: ${P(C) = 0,07}$
Pravděpodobnost, že nenastane vada C: ${P(C') = 1 - 0,07 = 0,93}$
Protože se jedná o nezávislé jevy, získáme pravděpodobnost toho, že daný výrobek nebude mít žádnou vadu (zde označené jako jev N), jako součin pravděpodobností, že nenastanou jednotlivé vady.
$${P(N) = P(A') \cdot P(B') \cdot P(C') = 0,95 \cdot 0,94 \cdot 0,93 = 0,83049 \doteq 0,83 }$$
Pravděpodobnost, že daný výrobek nebude mít žádnou vadu, bude 0,83.
Elektrický obvod obsahuje 6 spínačů, které náhodně nastavíme do stavu zapnuto nebo vypnuto. Jaká je pravděpodobnost, že obvodem bude procházet elektrický proud?
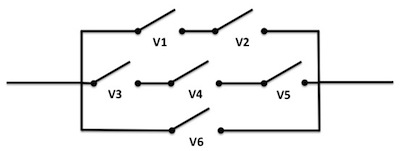
Každou větev elektrického obvodu budeme řešit samostatně. Vypínače v jedné větvi jsou nezávislé, tudíž budeme úkol řešit průnikem pravděpodobností a následně sjednotíme (sečteme) všechny paralelní větve.
Při výpočtu však musíme zohlednit fakt, že situace, pokud je aktivních více větví, je v daném součtu započítána vícekrát.
Již jsme používali vzorec pro sjednocení dvou náhodných jevů:
$${P(A \cup B) = P(A) + P(B) - P(A \cap B)}$$
Pro 3 náhodné jevy by vzorec byl upraven následovně:
$${P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C)}$$
Pravděpodobnost zapnutí jednoho vypínače je ${P(V) = \frac{1}{2}}$
Pro přehlednost si jednotlivé větvě obvodu označíme A (vypínače 1 a 2), B (vypínače 3, 4 a 5) a C (vypínač 6). Pravděpodobnosti, že těmito větvemi bude protékat proud, budou:
$${P(A) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}}$$
$${P(B) = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{8}}$$
$${P(C) = \frac{1}{2}}$$
Pravděpodobnost, že bude obvodem procházet elektrocký proud bude: $${P(O) = \frac{1}{4} + \frac{1}{8} + \frac{1}{2} - \frac{1}{4} \cdot \frac{1}{8} - \frac{1}{8} \cdot \frac{1}{2} - \frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{8} \cdot \frac{1}{2} = \frac{1}{4} + \frac{1}{8} + \frac{1}{2} - \frac{1}{32} - \frac{1}{16} - \frac{1}{8} + \frac{1}{64} = \frac{16 + 8 + 32 - 2 - 4 - 8 + 1}{64} = \frac{43}{64}}$$
Máme 2 nezávislé jevy A a B. Pravděpodobnost ${P(A \cap B) = 0,08}$, pravděpodobnost ${P(A) = 0,4}$. Určete pravděpodobnost B.
Protože se jedná o nezávislé jevy, musí platit: $${P(A \cap B) = P(A) \cdot P(B)}$$ $${0,08 = 0,4 \cdot P(B)}$$ $${P(B) = 0,2}$$
Máme 2 nezávislé jevy A a B. Pravděpodobnost ${P(A \cap B) = \frac{1}{8}}$, pravděpodobnost ${P(A \cap B') = \frac{1}{4}}$. Určete pravděpodobnost jevů A a B.
$${P(A \cap B) = P(A) \cdot P(B) = \frac{1}{8}}$$
$${P(A \cap B') = P(A) \cdot P(B') = \frac{1}{4}}$$
$${P(B') = 1 - P(B)}$$
$${P(A \cap B') = P(A) \cdot (1 - P(B)) = \frac{1}{4}}$$
Řešíme soustavu rovnic: $${P(A) \cdot P(B) = \frac{1}{8} \implies P(A) = \frac{1}{8\cdot P(B)}}$$ $${P(A) \cdot (1 - P(B)) = \frac{1}{4}}$$ $${\frac{1}{8\cdot P(B)} \cdot (1 - P(B)) = \frac{1}{4}}$$ $${1 - P(B) = \frac{8\cdot P(B)}{4}}$$ $${1 - P(B) = 2\cdot P(B)}$$ $${3\cdot P(B) = 1}$$ $${P(B) = \frac{1}{3}}$$
$${P(A) \cdot P(B) = \frac{1}{8}}$$ $${P(A) \cdot \frac{1}{3} = \frac{1}{8}}$$ $${P(A) = \frac{3}{8}}$$
Pravděpodobnost jevu A je ${\frac{1}{3}}$ a pravděpodobnost jevu B je ${\frac{3}{8}}$.