
a pravděpodobnost
PRAVDĚPODOBNOST
L13: Kombinatorické pravidlo součtu
<< Předchozí lekce | Seznam lekcí | Další lekce >>
Ve třídě je 18 děvčat a 12 chlapců. Kolikati způsoby mohou ve třídě vybrat jednoho zástupce do studentské rady, která funguje ve škole?
Žáci mohou vybrat z 18 děvčat nebo z 12 chlapců. Můžeme vybírat celkem ze 30 žáků. Pro počet způsobů výběru tedy platí:
$${ n = 18 + 12 = 30}$$
Zástupce do studentské rady mohou ve třídě vybrat 30 způsoby.
Ve třetím ročníku gymnázia studuje 86 žáků. 32 žáků má jako druhý jazyk němčinu, 15 francouzštinu, 12 španělštinu a zbytek ruštinu. Kolik žáků navštěvuje ruštinu?
Němčina ... 32 žáků
Francouzština ... 15 žáků
Španělština ... 12 žáků
Ruština ... x žáků
Dle kombinatorického pravidla součtu platí $${32 + 15 + 12 + x = 86}$$ $${59 + x = 86}$$ $${x = 86 - 59 = 27}$$
Ruštinu navštěvuje 27 žáků.

Matematická olympiáda (a + b) ... 32
Fyzikální olympiáda (b + c) ... 18
Obě olympiády (b) ... 10
Žádná soutěž (d) ... 50
V prvním ročníku je 90 žáků.
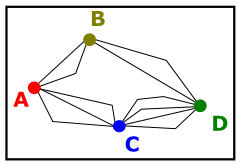
Přes město B: ${2 \cdot 2 = 4}$ cest
Přes město C: ${3 \cdot 4 = 12}$ cest
Celkem: ${4 + 12 = 16}$ cest
- Jak je definováno kombinatorické pravidlo součtu?
- Jak je definováno kombinatorické pravidlo součinu?
- V 1.A je 29 žáků. v 1.B 25 žáků a v 1.C 30 žáků. Kolikati způsoby lze vybrat z prvního ročníku jednoho žáka, který vystoupí na Vánoční akademii školy?
- Jsou-li ${{A_1}, {A_2}, \dots, {A_k}}$ konečné množiny, které mají po řadě {{n_1}, {n_2}, \dots, {n_k}} prvků a jsou li každé 2 disjunktní, potom počet prvků množiny ${{A_1} \cup {A_2} \cup \dots \cup {A_k}}$ je roven $${{n_1} + {n_2} + \dots + {n_k}}$$.
- Počet všech uspořádaných k-tic, jejichž první člen lze vybrat ${n_2}$ způsoby, druhý člen (po výběru prvního členu) ${n_2}$ způsoby, ... a k-tý člen (po výběru všech předcházejících členů) ${n_k}$ způsoby, je roven: $${{n_1}\cdot{n_2}\cdot~\dots~\cdot{n_k}}$$
- ${29 + 25 + 30 = 84}$