
a pravděpodobnost
PRAVDĚPODOBNOST
L12: Kombinatorické pravidlo součinu
<< Předchozí lekce | Seznam lekcí | Další lekce >>
Taneční kroužek navštěvuje 12 děvčat a 8 chlapců. Kolikati způsoby je možné vybrat 1 pár do taneční soutěže?
Děvče je možné zvolit jedním z 12 způsobů. Pro každé děvče je možné zvolit 8 způsoby chlapce. Celkový počet možností, jak vybrat pár do soutěže, bude:
$${ n = 12\cdot8 = 96}$$
Taneční pár do soutěže je možné vybrat 96 způsoby.
Výběr dvojic si můžeme názorně představit i pomocí tabulky, kde řádky tvoří prvky jedné kategorie (v případě predchozího příkladu děvčata) a sloupce tvoří druhá skupina (chlapci). Celkový počet dvojic je dán počtem buněk tabulky, jak je ukázano na následujícím příkladu:
Poznatek z předchozího příkladu lze samozřejmě zobecnit:
Dle pravidla součinu můžeme vybrat jednu ze dvou polévek. Ke každé volbě polévky jeden ze čtyř hlavních chodů a ke každé této dvojici jeden ze dvou nápojů. Počet možností výběru tedy bude: ${2 \cdot 4 \cdot 2 = 16}$
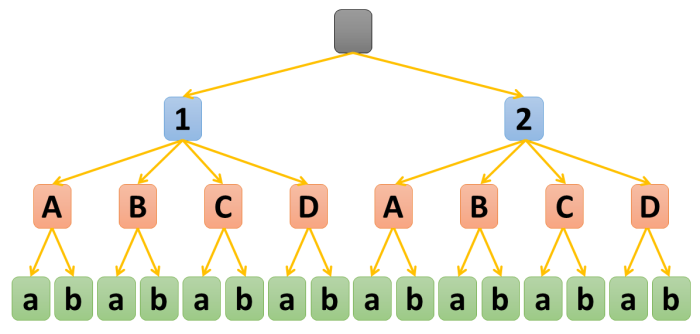
U příkladu L12.01 jsme si možnost volby vizualizovali pomocí tabulky. V případě více voleb můžeme využít i jiné grafické zobrazení, a tím je graf. Polévky si zobrazíme čísly 1 a 2, hlavní chody velkými písmeny A, B, C a D, nápoje potom malými písmeny a, b. Každá kombinace těchto znaků nám potom znázorňuje jednu volbu (např. 1Aa, 1Ab, ...). Naší situaci potom znázorňuje níže uvedený obrázek.
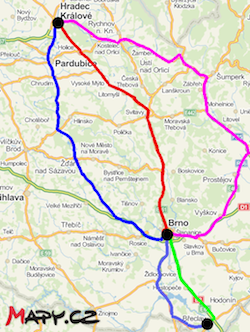
Z Hradce Králové do Brna lze použít jednu ze 3 tras, pro každou volbu trasy z Hradce Králové do Brna můžeme zvolit jednu ze dvou tras z Brna do Břeclavi. Když použijeme kombinatorické pravidlo součinu, dojdeme k následujícímu výsledku: ${3 \cdot 2 = 6}$
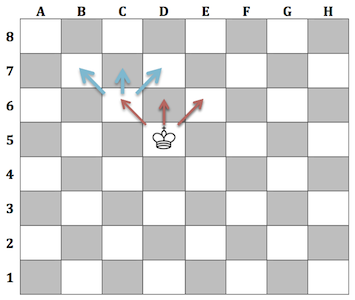
Král se musí dostat z 5. do 8. řady. Protože se může pohybovat pouze o jedno pole a musí zvolit trasu tak, aby se do 8. řady dostal na 3 tahy, tak z 5. do 6. řady má 3 možnosti pohybu. Pro každý takový tah má opět 3 možnosti pohybu z 6. do 7. a pro každý přesun z 6. do 7. může zvolit jednu ze tří cest do 8. řady. Použijeme-li pravidlo součinu, bude výsledek následující:
$${3 \cdot 3 \cdot 3 = 27}$$- Jak je definováno kombinatorické pravidlo součinu?
- Z města A do města B vede 5 cest, z města B do města C 3 cesty a z města C do města D 2 cesty. Kolika způsoby se můžeme dostat z města A do města D?
- Kolika způsoby může vybrat organizace, která má 40 členů, svého předsedu, místopředsedu a účetního, pokud každá osoba může zastávat nejvýše jednu funkci?
- Počet všech uspořádaných k-tic, jejichž první člen lze vybrat ${n_2}$ způsoby, druhý člen (po výběru prvního členu) ${n_2}$ způsoby, ... a k-tý člen (po výběru všech předcházejících členů) ${n_k}$ způsoby, je roven: $${{n_1}\cdot{n_2}\cdot~\dots~\cdot{n_k}}$$
- ${5 \cdot 3 \cdot 2 = 30 }$
- ${40 \cdot 39 \cdot 38 = 59~280}$