PRAVDĚPODOBNOST

10. řádek Pascalova trojúhelníku je tvořen kombinačními čísly $${\binom{10}{0}, \binom{10}{1}, \binom{10}{2}, \binom{10}{3}, \binom{10}{4}, \dots, \binom{10}{10}}$$

Díky platnosti vztahu ${\binom{n}{k} = \binom{n}{n-k}}$ není nutné počítat všechny hodnoty, protože hodnoty v Pascalově trojúhelníku jsou rozmístěny symetricky.

$${\binom{10}{0} = \binom{10}{10} = 1}$$

$${\binom{10}{1} = \binom{10}{9} = 10}$$

$${\binom{10}{2} = \binom{10}{8} = \frac{10!}{2!\cdot(10-2)!} = \frac{10!}{2!\cdot8!} = \frac{10 \cdot 9}{2} = 45}$$

$${\binom{10}{3} = \binom{10}{7} = \frac{10!}{3!\cdot(10-3)!} = \frac{10!}{3!\cdot7!} = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2} = 120}$$

$${\binom{10}{4} = \binom{10}{6} = \frac{10!}{4!\cdot(10-4)!} = \frac{10!}{4!\cdot6!} = \frac{10 \cdot 9 \cdot 8 \cdot 7}{4 \cdot 3 \cdot 2} = 210}$$

$${\binom{10}{5} = \frac{10!}{5!\cdot(10-5)!} = \frac{10!}{5!\cdot5!} = \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6}{5 \cdot 4 \cdot 3 \cdot 2} = 252}$$

Na 10. řádku Pascalova trojúhelníku budou hodnoty 1, 10, 45, 120, 210, 252, 210, 120, 45, 10 a 1.

Víme, že krajní hodnoty v Pascalově trojúhelníku jsou hodnoty 1 a každá další hodnota je součtem hodnot, které má v trojúhelníku nad sebou.

1. hodnota ... 1
2. hodnota ... 1 + 5 = 6
3. hodnota ... 5 + 10 = 15
4. hodnota ... 10 + 10 = 20
5. hodnota ... 10 + 5 = 15
6. hodnota ... 5 + 1 = 6
7. hodnota ... 1

Na 6. řádku Pascalova trojúhelníku budou hodnoty 1, 6, 15, 20, 15, 6 a 1.

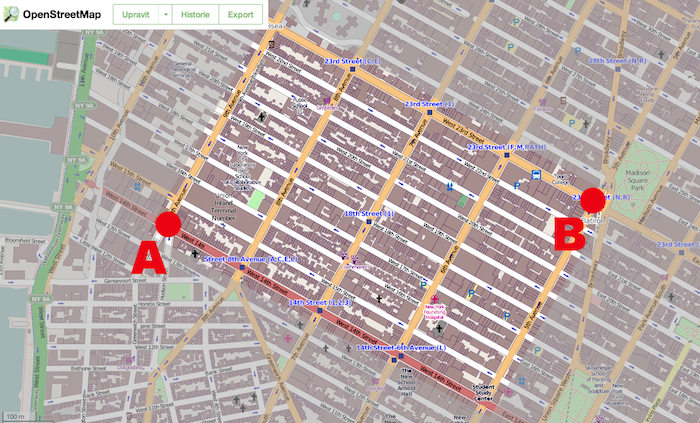
Pokud má daná síť m řádků a n sloupců platí, že počet cest je ${\binom{m + n}{n}}$ nebo ${\binom{m + n}{m}}$, kde m je počet čar mezi uzly ve vodorovném směru a n je počet čar mezi uzly ve svislém směru.

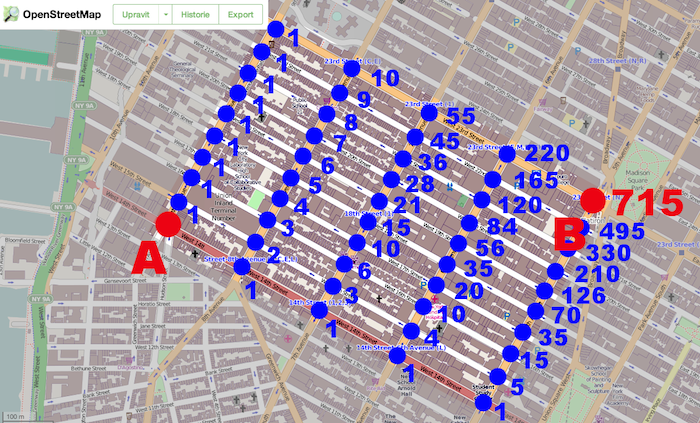
$${\binom{m + n}{n} = \binom{9 + 4}{9} = \binom{13}{9} = \frac{13!}{9! \cdot 4!} = 715}$$

Existuje 715 způsobů, jak se dostat z místa A do místa B tak, že se pohybujeme jen směrem doprava a nahoru (viz následující obrázek).

$${ (a^3 + b\sqrt{2})^4 = {6 \choose 0}\left(a^3\right)^6 + {6 \choose 1}\left(a^3\right)^5\left(b\sqrt{2}\right)^1 + {6 \choose 2}\left(a^3\right)^4\left(b\sqrt{2}\right)^2 + {6 \choose 3}\left(a^3\right)^3\left(b\sqrt{2}\right)^3 + {6 \choose 4}\left(a^3\right)^2\left(b\sqrt{2}\right)^4 + {6 \choose 5}\left(a^3\right)^1\left(b\sqrt{2}\right)^5 + {6 \choose 6}\left(b\sqrt{2}\right)^6 = }$$ $${ = a^{18}+ 6a^{15}b\sqrt{2} + 30a^{12}b^2 + 40a^9b^3\sqrt{2} + 60a^6b^4 + 24a^3b\sqrt{2} + 8b^6 }$$

$${\left(\sqrt{3} - \sqrt{5}\right)^4 = {4 \choose 0}\left(\sqrt{3}\right)^4 + {4 \choose 1}\left(\sqrt{3}\right)^3\left(-\sqrt{5}\right)^1 + {4 \choose 2}\left(\sqrt{3}\right)^2\left(-\sqrt{5}\right)^2 + {4 \choose 3}\left(\sqrt{3}\right)^1\left(-\sqrt{5}\right)^3 + {4 \choose 4}\left(-\sqrt{5}\right)^4 = }$$ $${= 1\cdot9 - 4\cdot3\sqrt{3}\sqrt{5} + 6\cdot3\cdot5 - 4\sqrt{3}\cdot5\sqrt{5} + 1\cdot25 = 9 - 12\sqrt{15} + 90 - 20\sqrt{15} + 25 = 124 - 32\sqrt{15}}$$

$${ {14 \choose 8 - 1}\left(\frac{x^3}{y^5}\right)^{14 - (8 - 1)}\left(-\frac{y^4}{x}\right)^{8 - 1} = {14 \choose 7}\left(\frac{x^3}{y^5}\right)^{7}\left(-\frac{y^4}{x}\right)^{7} = -{14 \choose 7}\cdot\frac{x^{21}}{y^{35}}\cdot\frac{y^{28}}{x^{7}} = -{14 \choose 7}\cdot x^{14}\cdot y^{-7} }$$

$${ {16 \choose 13 - 1}\left(\sqrt[2]{x}\right)^{16 - (13 - 1)}\left(\frac{\sqrt[3]{y}}{2}\right)^{13 - 1} = {16 \choose 12}\left(\sqrt[2]{x}\right)^{4}\left(\frac{\sqrt[3]{y}}{2}\right)^{12} = {16 \choose 12} \cdot x^2 \frac{y^4}{2^{12}} = \frac{16!}{12!\cdot4!}\cdot\frac{x^2y^4}{4096} = \frac{16\cdot 15\cdot 14\cdot 13}{24}\cdot\frac{x^2y^4}{4096} = \frac{455}{1024}\cdot x^2y^4}$$

Číslo 1,02 můžeme zapsat jako součet ${\left(1 + \frac{2}{100}\right)}$.

Řešíme tedy binomický rozvoj $${\left(1 + \frac{2}{100}\right)^{8}}$$

$${\left(1 + \frac{2}{100}\right)^{8} = {8 \choose 0}1^{8} + {8 \choose 1}1^{7}\left(\frac{2}{100}\right)^1 + + {8 \choose 2}1^{6}\left(\frac{2}{100}\right)^2 + {8 \choose 3}1^{5}\left(\frac{2}{100}\right)^3 + \dots = 1 + 8\cdot\frac{2}{100} + 28\cdot\frac{4}{10~000} + 26\cdot\frac{8}{1~000~000} \dots }$$ $${= 1 + 0,16 + 0,0112 + 0,000224 + \dots = 1,171424 \doteq 1,17}$$

Pozn: Použili jsme pouze první 4 členů binomického rozvoje, protože u požadované přesnosti na setiny nám již další členy výsledek neovlivní.

Budeme uvažovat vzorec pro k-tý člen binomického rozvoje: $${ {n \choose k - 1}a^{n - (k - 1)}b^{k - 1} }$$

Tedy: $${ {28 \choose k - 1}\left(2x^5\right)^{28 - (k - 1)}\left(3x^6\right)^{k - 1} = {28 \choose k - 1}\left(2x^5\right)^{29 - k}\left(3x^6\right)^{k - 1} = {28 \choose k - 1}\cdot 2^{29 - k}\cdot x^{5(29 - k)}\cdot 3^{k - 1}\cdot x^{6(k - 1)} = }$$ Výraz ${{28 \choose k - 1}\cdot(2^{29 - k}\cdot 3^{k - 1}}$ nahradíme konstantou ${C}$, protože se bude jednat o konstantní hodnotu a proměnnou ${x}$ neovlivní. $${ = C\cdot x^{5(29 - k)}\cdot x^{6(k - 1)} = C \cdot x^{5(29 - k) + 6(k - 1)} = C \cdot x^{139 + k} }$$

Člen ${x^{139 + k}}$ musí být roven roven ${x^{150}}$. Řešíme tedy rovnici: $${x^{139 + k} = x^{150}}$$ $${139 + k = 150}$$ $${k = 11}$$

Proměnnou ${x^{105}}$ nebude obsahovat 11. člen daného binomického rozvoje.

Zapíšeme vzorec pro 3. člen binomického rozvoje a porovnáme jej s požadovanou hodnotou. $${{8 \choose 3 - 1}1^{8 - (3 - 1)}x^{3 - 1} = 7\cdot 10^{-6}}$$ $${{8 \choose 2}1^{6}x^{2} = 7\cdot 10^{-6}}$$ $${28x^{2} = 7\cdot 10^{-6}}$$ $${x^{2} = \frac{7}{28}\cdot 10^{-6}}$$ $${x^{2} = \frac{1}{4}\cdot 10^{-6}}$$ $${x = \pm \frac{1}{2}\cdot 10^{-3}}$$