a pravděpodobnost
PRAVDĚPODOBNOST
L01: Faktoriál
Použití tohoto vztahu lze ilustrovat na jednoduchém příkladu:
Určete hodnotu ${{6!}}$
$${6! = 6\cdot5\cdot4\cdot3\cdot2\cdot1 = 720}$$
Kromě přirozených čísel je faktoriál definován i pro hodnotu 0.
Poznámka: Faktoriál budeme zatím chápat pouze jako matematickou operaci. Postupně se však dostaneme k jeho aplikaci v kombinatorice.
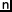. Kvůli problémům s tiskem tohoto operátoru byl následně nahrazen zápisem n!, který se používá dodnes.Určete, kolikati nulami bude končit číslo ${{70!}}$
U vyšších faktoriálů si s kalkulačkou už asi nevystačíme. Pokud bychom použili výpočetní techniku a výpočet svěřili serveru Wolfram Alpha zjistíme, že hodnota 70! je 11 978 571 669 969 891 796 072 783 721 689 098 736 458 938 142 546 425 857 555 362 864 628 009 582 789 845 319 680 000 000 000 000 000 (nebo přibližně ${1.197857\cdot10^{100}}$). Z této hodnoty už jednodušše zjistíme, že dané číslo má 16 nul.
Né vždy však máme k dispozici moderní techniku, proto zkusme k tomuto výsledku dojít logickou úvahou:
- Počet nul ve výsledném čísle ovlivní násobky desítky (v čísle 70! je to 10, 20, 30, 40, 50, 60 a 70) ... touto úvahou dojdeme k tomu, že dané číslo bude obsahovat 7 nul
- Dále bude počet nul ovlivňovat součin čísel ${2\cdot5}$, rozhodující tedy bude také počet násobků čísla 5 v součinu čísel od 1 do 70. Tyto násobky jsou 5, 15, 25, 35, 45, 55 a 65 (čísla 10, 20, ... jsme vynechali, protože ty už jsou uvažovány v předchozím bodě). Těch je také 7
- Počet nul navíc ovlivní ještě čísla 25 a 50, které mají ve svém prvočíselném rozvoji číslo 5 dvakrát. Tím přidáme do výsledku další 2 nuly.
- Počet nul bude 16.
Jak už bylo zmíněno, pro všechna přirozená čísla je faktoriál čísla n součinem čísel 1 až n. Jak to tedy bude vypadat s hodnotou faktoriálu? Můžeme se přesvědčit na níže uvedených hodnotách:
Faktoriál přirozeného čísla pro hodnoty 0 až
Z výše uvedeného příkladu lze vidět, že faktoriál lze pro menší hodnoty určit bez problémů, ale se zvyšující se hodnotou n hodnota faktoriálu roste velmi rychle. Z tohoto důvodu si při řešení výrazů s faktoriály můžeme pomoci pomocí následujícího pravidla, které nám usnadní nejen zjednodušování výrazů, ale i řešení rovnic.
Platí, že jakýkoliv faktoriál můžeme zapsat ${n! = n\cdot(n-1)! = n\cdot(n-1)\cdot(n-2)! = \dots}$
Použití tohoto vztahu lze ilustrovat na jednoduchém příkladu:
Zjednodušte výraz $${{8!\cdot4!}\over{10!}}$$
$${{{8!\cdot4!}\over{10!}} = {{8!\cdot4!}\over{10\cdot9\cdot8!}} = {{4\cdot3\cdot2\cdot1}\over{10\cdot9}} = {{4\cdot3\cdot1\cdot1}\over{5\cdot9}}= {{4\cdot1\cdot1\cdot1}\over{5\cdot3}} = {{4}\over{15}}}$$
Zjednodušte výraz $${{9! + 2\cdot7!}\over{8! - 9!}}$$
$${{{9! + 2\cdot7!}\over{8! - 9!}}= {{9\cdot8\cdot7! + 2\cdot7!}\over{8! - 9\cdot8!}} = {{2\cdot7!\cdot(9\cdot4 + 1)}\over{8!\cdot(1 - 9)}} = {{2\cdot7!\cdot(9\cdot4 + 1)}\over{8\cdot7!\cdot(-8)}} = {{(9\cdot4 + 1)}\over{4\cdot(-8)}} = -{{37}\over{32}}}$$
Porovnejte hodnoty následujících zlomků $${{{(3^2)!}\over{(3!)^2}}~~a~~{{(3!)^2}\over{(3)^2!}}}$$
Abychom mohli hodnoty daných výrazů porovnat, je nutné je nejprve upravit.$${{{(3^2)!}\over{(3!)^2}} = {{9!}\over{(3\cdot2\cdot1)^2}} = {{9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}\over{(3\cdot2\cdot1)^2}} = {{9\cdot8\cdot7\cdot6\cdot5\cdot4}\over{3\cdot2\cdot1}} = {{9\cdot8\cdot7\cdot6\cdot5\cdot4}\over{6}} = 10080}$$
$${{{(3!)^2}\over{(3)^2!}} = {{(3\cdot2\cdot1)^2}\over{9!}} = {{(3\cdot2\cdot1)^2}\over{9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}} = {{3\cdot2\cdot1}\over{9\cdot8\cdot7\cdot6\cdot5\cdot4}} = {{6}\over{9\cdot8\cdot7\cdot6\cdot5\cdot4}} = {{1}\over{10080}}}$$
$${{{(3^2)!}\over{(3!)^2}}~~>~~{{(3!)^2}\over{(3)^2!}}}$$
- Jak je definován faktoriál přirozeného čísla?
- Jakou hodnotu má faktoriál čísla 0?
- Určete, kolik nul bude mít číslo 56!
- Vypočítejte: $${{2\cdot(8! + 7!)}\over{3!\cdot6!}}$$
- ${n! = n\cdot(n-1)\cdot(n-2)\cdot\dots\cdot2\cdot1}$
- ${0! = 1}$
- 13 nul
- 21